Does the Orientation of a Vector Shows Its Direction
The vector space Λ nV called the top exterior power therefore has dimension 1. A quick example of orientation is a simple line curve.

Vectors Direction Orientation Addition Multiplication Scalars
An orientation is just such a choice.

. Lets start with a circle and duplicate it. It will be the unit vector in the direction of. This central axis is defined for both objects and the part of each axis interior to its respective object is parameterized from 0 to 1.
That is Λ nV is just a real line. For example velocity is a vector. Scale the second one down and combine the two via Path Difference.
The sense clears this ambiguity and indicates where the arrowhead actually goes. The vector space Λ nV called the top exterior power therefore has dimension 1. The direction in which each vector points determines its orientation.
Use the right hand rule. I think you mean Is the concept of orientation of a vector related to the concept of its direction. You see the direction your article uses the word orientation just gives you an angle that the vector makes with the horizontal axis but that creates an ambiguity since an arrow can point in two opposite directions and still make the same angle.
If it is 0 the unit vectors are perpendicular to each other. Direction the orientation of a vector shows its always true In the absence of air friction the horizontal component of a projectiles velocity doesnt change as the projectile moves 8 units Which best approximates the resultant of a pair of 6 unit vectors at right angles to each other. This is a real vector space of dimension.
Their orientations cannot change a the value of scalar b a vector or d the magnitude of a vector. If the dot product is 1 the two unit vectors are pointing exactly at the same direction. The result is a ring.
It can be observed as the slope of the line it lies on this is because its slope is calculated in the same way we calculate the slope of a line. Duplicate the line and select a node. So the orientation tells you what angle the vector is and the.
The direction of a vector is the measure of the angle it encloses with the y axis. The dot product has a property of telling if two unit vectors are in parallel and if not how much they differ. That is a linear vector space must also be an inner-product space.
There is no a priori choice of which direction on this line is positive. A vector actually represents 2 things. Yes a vector can be represented in terms of a unit vector which is in the same direction as the vector.
The direction of vis arc tan 43. We will mark the direction of a vector with varphi. Velocity is an example of a vector.
A direction and a distance or length. The direction of your thumb is the outward direction. That is Λ nV is just a real line.
This is a real vector space of dimension. This angle will vary if the orientation of axes is changed. In addition the user defines an orientation vector or a default direction is used that is perpendicular to the axis see Figure 433.
Adam Higgins Jan 15 2019 at 1735. This is a real vector space of dimension n k. The direction of a vector is the orientation of the vector that is the angle it makes with the x-axis.
It will be the unit vector in the direction of. There is no a priori choice of which direction on this line is positive. Sign in to download full-size image Figure 433.
If a vector has a length of exactly 1 unit it is called a. With an arrow at the top but another fixed point at the other end a vector may be shown. That is Λ nV is just a real line.
There is no a priori choice of which direction on this line is positive. A vector is drawn by a line with an arrow on the top and a fixed point at the other end. Its distance is its length from its tail to its head.
Orientation quaternion Main article. The vector space Λ nV called the top exterior power therefore has dimension 1. In convention where its vector diagram represents a vector its direction is determined by the counterclockwise angle it makes with the positive x-axis.
The direction in which the arrowhead of the vector is directed gives the direction of the vector. So any values above 0 means that the unit vectors are going in roughly the same. However as pointed out by another respondent either property depends on the existence of a scalar product.
Imagine putting the index finger and middle finger at right angles to each other within the plane and your thumb at right angles to both. A vector diagram will show the direction of the force as well as its magnitude. For any n -dimensional real vector space V we can form the k th- exterior power of V denoted Λ kV.
Yes a vector can be represented in terms of a unit vector which is in the same direction as the vector. But when a vector is resolved along axes the component is dependent on the angle between the vector and the axis along which it is being resolved. The vectors direction is determined by the arrowheads point of departure.
Orientation and sense together determine the direction of a vector. Click on Path Reverse and the direction of thick to thin changes. The number of dimensions with which youre working also changes your terminology a bit depending on how you would describe that chirality.
Its direction is indicated by the arrow at its head. The sense of a vector is specified by the order of two points on a line parallel to the vector. A vectors orientation or the angle it creates with the x-axis determines its direction.
The answer is yes if a vector is assumed to possess either property. Quaternions and spatial rotation Another way to describe rotations is using rotation quaternions also called versors. The green vector represents the same direction as the blue vectors but it has a different length.
The taper stroke goes from thick to thin. For any n -dimensional real vector space V we can form the k th-exterior power of V denoted Λ kV. The orientation of a vector is specified by the relationship between the vector and given reference lines andor planes.
Orientation may be visualized by attaching a basis of tangent vectors to an object. Two dimensions use clockwise and counter-clockwise and three dimensions use left-handed and right-handed Direction is a bit more simple than that. A vector quantity is represented by a vector diagram and hence has a directionthe orientation at which the vector points is specified as the direction of a vector.
Orientation pertains to the chirality of the vector.

2 2 Coordinate Systems And Components Of A Vector University Physics Volume 1
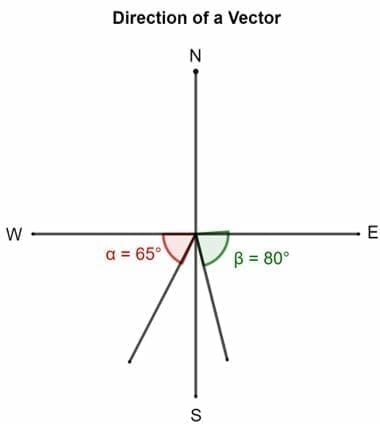
The Direction Of A Vector Explanation And Examples

Vectors Direction Orientation Addition Multiplication Scalars

Direction Of A Vector Formula What Is Direction Of Vector Formula
No comments for "Does the Orientation of a Vector Shows Its Direction"
Post a Comment